---

главная написать автору

Обоснование существования эфироопорных сил в классической электродинамике

Это физико-математическое обоснование появилось как приложение к письму в адрес руководства предприятием, занимающимся космическими летательными аппаратами. Оно в концентрированном виде  содержит  решения  вопросов, достаточных для получения однозначных заключений, согласно которым эфироопорное движение существует как прямое следствие фундаментальных положений классической электродинамики и общей физики, вот почему представляет интерес для физиков, инженеров, студентов и лиц, занимающихся исследованиями в области классической электродинамики.

Введение

    В период становления классической электродинамики и теории относительности о силах, называемых в этой работе «эфироопорными» ничего не было известно. Первые сведения появились в 30-х годах в монографии И. Е. Тамма до сих пор являющейся популярным учебным пособием по классической электродинамике в России [9]. Там был описан мысленный эксперимент, послуживший прототипом натурального опыта, выполненного в конце 70-х годов канадскими физиками Грехемом и Лахозом [11].  Цилиндрический конденсатор, между обкладками которого ничего не было, помещали в сильное внешнее магнитное поле. При подаче на обкладки переменного напряжения регистрировали механические колебания конденсатора, по мнению авторов, свидетельствующие о наличии силы реакции на вакуум. Пейдж и Адамс в 1945 году установили [1], что равнодействующая сила, возникающая при взаимодействия движущихся зарядов между собой, не равна нулю. Они показали, что закон сохранения импульса будет выполняться в предположении, что статические электромагнитные поля обладают собственным импульсом (количеством движения) и дали формулу для вычисления этой величины. Однако, согласно настоящей работе, эта величина не сохраняется при ускоренном движении зарядов (а также при изменении магнитных моментов), в силу чего её нельзя отождествлять с импульсом электромагнитного поля. Она имеет другой физический смысл – служит мерой силового и энергетического взаимодействия вещества (в форме движущихся зарядов и магнитных материалов) с физическим вакуумом, обеспечивая возможность осуществления непрерывного ускоренного движения в космическом пространстве. 

    Причина, по которой работы первых авторов (Тамма, Пейджа и Адамса, Грехема и Лахоза и др.), в своё время, не получили должной оценки и развития состоит в следующем. Согласно представлениям основоположников классической электродинамики Максвелла, Лоренца, Пуанкаре (и др.) и их многочисленных последователей (живущих и поныне во всех странах мира) эфир - это своеобразная форма материи, заполняющая всё физическое пространство, как ни микроуровне (внутри и атомов, молекул и т. д.) так и на макроуровне (пространство между звёздами, галактиками и т. п). Даже Эйнштейн, автор специальной теории относительности (СТО), признавал существование эфира, о чём свидетельствует его статья «Эфир и теория относительности», цитирую оттуда: - «пространство немыслимо без эфира; действительно, в таком пространстве не только было бы невозможно распространение света, но не могли бы существовать масштабы и часы и не было бы никаких пространственно-временных расстояний в физическом смысле слова». Однако в истории физики случилось так, что получила сильное распространение другая точка зрения, согласно которой «эфир физике не нужен», его следует «похоронить» и, значит, какие бы то ни были взаимодействия с эфиром исключены. Так считает школа релятивизма, философия и идеология которой базируется на постулатах, т. е. принимаемых без доказательства догмах. Так как идеология школы релятивизма в наше время преобладает, то всякие научные исследования, касающиеся взаимодействия эфира (физического вакуума) с веществом на макроскопическом уровне сильно затруднены противодействием этой школы. Всё, что выходит за рамки идеологии релятивизм, считается парадоксальным и не имеет никаких шансов научного объяснения в этих рамках. Теория относительности, совмещённая с существованием эфира, создана Г. А. Лоренцем и Пуанкаре раньше теории Эйнштейна. Она имеет тот же самый математический аппарат, который используется в наше время в СТО Эйнштейна, но, в то же время, позволяет ставить и решать задачи, далеко выходящие за рамки релятивизма. С основами теории относительности Лоренца можно познакомиться по его книге "Г. А. Лорентц. Теория электронов, М., 1953" и др. литературным источникам.

Эфироопорные силы могут иметь место в разных макроскопических системах, при наличии колебаний электрического и магнитного полей. Ниже рассмотрены некоторые   варианты, которые, по мнению автора, наиболее удобны для развёртывания научно-исследовательских работ и опытно-конструкторских разработок, с целью их практического  применения на транспорте и в энергетике.

1. Эфироопорные силы в токо-зарядовых системах

            К токо-зарядовым системам относятся всевозможные резонаторы и вибраторы. Без существенного ограничения общности можно обойтись рассмотрением квазистатических систем, в которых токи и напряжения (а также дипольные моменты) совершают синфазные гармонические колебания. Геометрические размеры малы по сравнению с длиной волны, соответствующей частоте колебаний системы. Такие системы разбиваются на малые части (объёмы), в которых образуемые электронной компонентой отрицательные заряды, колеблются около неподвижных центров, образуемых ионной компонентой или элементами кристаллической решётки, что позволяет рассматривать их (эти системы) как суперпозицию пар колеблющихся с одинаковыми частотами диполей. Результирующая сила системы отыскивается путём суммирования (интегрирования) по таким парам диполей, что проводит к простым решениям в некоторых практически важных случаях.

При таком подходе, дипольные моменты р и их производные по времени

При таком подходе, дипольные моменты р и их производные по времени  и обусловлены движением зарядов (заключённых в малых объёмах вещества), что позволяет пользоваться формулами для полей, создаваемых движущимися зарядами.

= qv , = qw

где q – заряд, v - скорость, w – ускорение.

            Меняющийся диполь также можно рассматривать как элемент тока,  = qv ® Idl (dl – элемент длины), что удобно при интегрировании по объёму, занятому проводником. 

            Скорости зарядов в рассматриваемых нами резонаторах и вибраторах заведомо малы по сравнению со скоростью света v << c и это приближение мы будем использовать в наших расчётах. Размеры вибраторов (а) всегда малы по сравнению с длинами волн, соответствующих их частотам колебаний? а << l, что соответствует квазистатическому режиму их работы. В наших задачах квазистатическое приближение  годится и для  оценок  (с достаточно хорошей точностью) сил в резонаторах.

Пусть два заряда q₁ и q₂ движутся со скоростями v₁, v₂ и ускорениями w₁, w₂. Определим  силы, действующие на  каждый их этих зарядов и суммарную силу – равнодействующую системы двух зарядов. В процессе движения каждый из зарядов испытывает действие силы Лоренца, со стороны образуемого другим зарядом магнитного поля. Отсюда путём непосредственных вычислений  приходим к известной с 1945 года [1] формуле равнодействующей магнитных сил Лоренца системы:

            (1)

Её можно переписать в форме, содержащей скорости изменений дипольных моментов

           (1а)

Или в форме, содержащей элементы токов

        (1b)

            Кроме магнитной силы Лоренца, на образующие колеблющиеся диполи движущиеся заряды действует электрическая сила Лоренца - это кулоновская сила, сила зависящая от скорости, и сила, зависящая от ускорения заряда.

            В квазистатическом приближении напряжённость электрического поля кулоновской и зависящей от скорости компонент, как известно [2], описывается формулой:

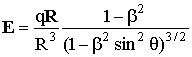              (2)

где b = v/c, q - угол между направлением движения и радиус-вектором R.

Учитывая малость параметра b (v << c), и соотношение

b² sin²q = (b x n)² = b² - (bn)²

где n -  единичный вектор в направлении R,

формулу (2) можно переписать в виде:

          (3)

Если в правой части этой формулы раскрыть квадратные скобки, то первый член отвечает создаваемому зарядом кулоновскому полю (не зависящему от скорости). Кулоновская сила F₂₁ (F₁₂), действующая на первый (второй) диполь р₁ (р₂) со стороны второго (первого) диполя р₂ (р₁) определяется по формуле:

         (4)

Вычисляя, найдём, что сумма кулоновских сил, с которыми два диполя действуют друг на друга, равна нулю (F₁₂ + F₂₁ = 0), что вполне понятно, потому эта сила численно равна кулоновской равнодействующей между неподвижными зарядами. *)

Так как второй член правой части (3) отличается от первого только не зависящим от R множителем, то обусловленная им суммарная сила тоже равна нулю.

Определим теперь,   какая сила, F_e, действует на диполь со стороны электрического поля, обусловленного третьим членом формулы (3). Согласно общей формуле  F_e = (pÑ)E, где  p = qd – дипольный момент, d – амплитуда отклонения заряда от равновесного положения, E – напряжённость электрического поля, которую можно переписать в виде:

E = -3q(bn)²R/2R³ = -3q(vR)²R/2R⁵

Отсюда, для силы, действующей на диполь p₂ = q₂d₂ со стороны движущегося со скоростью v₁ заряда q₁, получим:

      (5)

Аналогичная сила F_e21 действует на диполь p₁ = q₁d₁ со стороны движущегося со скоростью v₂ заряда q_2.

Максимальная величина суммы этих сил получится, если выражение в фигурных скобках (5) заменить суммой модулей слагаемых, в каждом из которых скалярные произведения заменить на произведение модулей сомножителей. Тогда получим:

(6)

Из (1) следует, что максимальное значение силы Лоренца равно:

       (7)

Отношение электрической и магнитной компонент, согласно (6) и (7) будет равным:

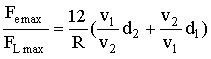          (8)

            Так как дипольные моменты по условию задачи колеблются синфазно, то справедливо соотношение  v =  wd, откуда следует, что

F_{e max}/F_{L max} = 12(d₁ + d₂)/R     

Не нарушая общности результата, можно предположить, что в этом выражении d₁ = d₂ = d. Тогда получим:

F_{e max}/F_{L max} = 24d/R

Отсюда видно электрическая сила F_e пренебрежимо мала по сравнению с магнитной силой Лоренца. Действительно, к примеру, в СВЧ диапазоне R соизмеримо с длиной волны (измеряется сантиметрами), а амплитуда смещения d измеряется нанометрами – разница до семи порядков.      

Перейдём к силам, обусловленным ускоренным движением зарядов.  Пусть два заряда q₁ и q₂ движутся с малыми по сравнению со световой скоростями v₁ << c,  v₂ << c и с произвольными ускорениями w₁, w₂. Если учитывать запаздывание с точностью до членов второго порядка малости по v/c, то удобно пользоваться потенциалами Дарвина [6, § 65], согласно которым, поля, обусловленные движением, определяются только векторным потенциалом:

                         (9)

где R – расстояние от заряда до точки наблюдения.

В процессе движения каждый из зарядов создаёт в окружающем пространстве обусловленное ускорением электрическое поле

                       (10)

Перейдём в неинерциальную систему отсчёта  (НСО), в которой заряд q₁ имеет нулевое ускорение. Тогда по отношению к нему заряд q₂ движется с ускорением   w₂ -  w₁ и, в соответствии с (10) действует на заряд  q₁ с силой F₁₂, равной

                   (11)

Эта сила войдёт в уравнение движение заряда q₁ и останется там после возвращения в первоначальную инерциальную систему отсчёта. Обратим наше внимание на второй член правой части (11) и «переведём» его содержание с математического языка на русский. У нас получится следующее: - «сила, действующая на ускоренный заряд  q₁ в присутствии другого заряда q₂, равна по величине противоположна по направлению той, обусловленной ускорением силе, с которой заряд  q₁ действует на заряд q₂.  Эту силу можно получить и другим способом, путём разложения давно известной магнитодинамической силы, действующей на меняющийся магнитный момент в электрическом поле (см. ниже формулу (20) с прилегающим текстом). Вот почему целесообразно называть её «зарядовой магнитодинамической силой, в отличие от известной магнитно-дипольной магнитодинамической силы.  С другой стороны, сила, определяемая первым членом  правой части (11), будучи проинтегрированной по замкнутому контуру даст известную электрическую силу индукции, действующую на заряды вследствие изменения магнитного момента, в связи с чем, её целесообразно называть «зарядовой силой индукции». Таким образом, сила, действующая на ускоренный заряд со стороны другого ускоренного заряда, есть сумма силы индукции F_i и магнитодинамической силы  F_md.

F = F_i + F_md                    (12)

По аналогии с (11) запишем силу, действующую на второй заряд со стороны первого:

               (13)

Складывая (11) и (13), получим 0 

F₁₂ + F₂₁ = 0                      (14) 

Таким образом, все возможные электрические силы взаимодействия в системе двух движущихся зарядов (колеблющихся диполей, элементов переменного тока) либо взаимно компенсируются (обнуляются), либо пренебрежимо малы по сравнению с суммарной магнитной силой Лоренца (Ампера) (1), (1a), (1b), которая представляет собой равнодействующую рассматриваемой системы. Отсюда следует простое правило: -
«Чтобы определить равнодействующую отдельно взятого устройства (типа резонатора или вибратора), достаточно посчитать результирующую силу Ампера, отыскание которой  во многих практически важных случаях  не представляет серьёзных затруднений.

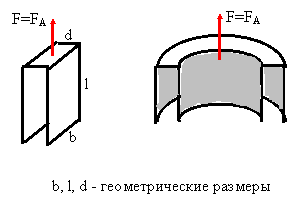На рисунке изображены  П-образный и цилиндрический резонаторы, результирующая сила Ампера в которых определяется путём простого интегрирования и приводит к следующим результатам для амплитудного значения (в системе СИ): для П-образного резонатора

        (15)

где e₀ – электрическая постоянная, U – напряжение на концах резонатора. Для цилиндрического резонатора

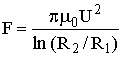(16)   

где m₀ – магнитная постоянная, R₁, R₂ – радиусы внутреннего и внешнего цилиндров.

Однако, более подробные исследования, проведённые с привлечением экспериментальных данных, показали, что формулы (15), (16), нельзя применять к металлическим устройствам типа изображённых на рисунке резонаторов и вибраторов, потому что индуцированные заряды (их можно вычислить, к примеру, методом зеркальных отражений) будут компенсировать силы, вызванные токами, создаваемыми активными зарядами. Подробности см. в статье

http://www.tts.lt/~nara/exper.pdf

2. Эфироопорные силы в магнитно-зарядовых системах

Магнитно-зарядовые системы содержат движущиеся заряды и диэлектрические магнитные материалы (магнитные сердечники). Простейшая из них включает в себя токовый магнитный диполь и движущийся заряд. Вначале, рассмотрим случай, когда магнитный диполь покоится в лабораторной системе отсчёта, а электрический заряд движется относительно него со скоростью v. Если в качестве магнитного диполя принять контур с током малых размеров (по сравнению с расстоянием до заряда), то равнодействующую можно определить как суммарную силу Лоренца, образуемую при взаимодействии движущегося заряда с элементами контурного тока, в соответствии с формулами (1), (1b). При этом конечная формула в точности совпадает с результатом непосредственного вычисления силы, действующей на элементарный токовый магнитный диполь с магнитным моментом m в поле движущегося заряда. См. ссылки

http://ivanov-georgij2010.narod.ru/amper/neutron.html

( http://www.tts.lt/~nara/lagrang/lagrang.htm )

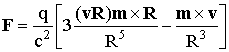
где v – скорость движения заряда  q относительно магнитного диполя, R – расстояние между частицами, отсчитываемое от магнитного диполя. Эту формулу можно записать в более компактном виде

(18)

где  = dE /dt – скорость изменения напряжённости электрического поля в точке нахождения магнитного диполя.

Теперь рассмотрим другой частный случай, при котором обе частицы (заряд и магнитный диполь) относительно неподвижны, а магнитный момент магнитного диполя меняется со временем.  Тогда на заряд будет действовать сила индукции F_i, обусловленная электрическим полем индукции, возбуждаемым меняющимся магнитным моментом  магнитного диполя, легко вычисляемая по известной формуле  F_i = - (1/с)¶A/¶t, где  A = (m x R)/R³ – векторный потенциал магнитного диполя. Отсюда получим:

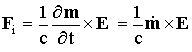    (19)

            Теперь определим, какая сила будет действовать на меняющийся магнитный диполь в электрическом поле постоянного заряда. Для этого решим следующую вспомогательную задачу:

Пусть в однородном постоянном электрическом поле Е движется магнитный диполь m со скоростью v. Построим его функцию Лагранжа и напишем уравнение движения. Какая скорость не имеет значения. Она может быть даже нулевой, потому что, как мы увидим ниже, важна не скорость, а её производная, которая может отличаться от нуля, даже при нулевой скорости.

Функция Лагранжа L есть разность между кинетической энергией магнитного диполя Т и его потенциальной энергией П = -(mH), H – напряжённость магнитного поля, в вакууме, совпадающая с индукцией (в гауссовой системе). Перейдём в систему отсчёта, в которой магнитный диполь покоится. Тогда, в соответствии с преобразованиями Лоренца, там будет магнитное поле H = - c^-1v x E. Потенциальная энергия будет равной,

П = c^-1m (v x E) = - c^-1v (m x E)

Так как потенциальная энергия при малых скоростях одинакова во всех ИСО, то она останется той же самой и в системе отсчёта, в которой магнитный диполь движется с заданной начальной скоростью v.

Можно рассуждать и по-другому. Движущийся магнитный диполь m образует электрический диполь p по формуле p = - c^-1(m x v) [6]. Отсюда получим

П = - рЕ = c^-1E (m x v) = - c^-1v (m x E)

Теперь можно записать функцию Лагранжа

L = T + c^-1v(m x E)

Как видим L, совсем не зависит от координат. Это значит, что (d/dt)(∂L/∂v) = 0

где   - сила, - скорость изменения магнитного момента магнитного диполя.

Отсюда получаем искомое уравнение движения

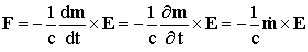          (20)

Мы получили известное из работ классиков (Эйнштейна и Лауба [5], де Гроота и Сатторпа [6]) выражение для магнитодинамической силы.  

Сравнивая (19) и (20), приходим к заключению, что действующая на заряд электрическая сила индукции в точности компенсируется действующей на магнитный диполь магнитодинамической силой. Следовательно, сила Лоренца (Ампера), согласно формуле (18) есть полная равнодействующая системы, в которой заряд движется с произвольной (малой по сравнению со световой) скоростью в поле магнитного диполя, меняющего свой магнитный момент:

[18]

            Согласно этой формуле, если магнитный момент и скорость изменения электрического поля меняются синфазно, то в системе (замкнутой по традиционным понятиям) возникает постоянная по направлению сила. Действительно, пусть магнитный момент меняется по закону m = m₀ cos wt, а электрическое поле по закону  E = E₀ sin wt, тогда . Если направления векторов m и E взаимно перпендикулярны, то подставляя в (18), получим силу F = wm₀E₀ cos² wt, среднее значение которой равно:

<F> = wm₀E₀/2с (21)

Отсюда видно, что система будет совершать инфинитное (неограниченное) ускоренное движение в заданном направлении.

Такое движение может быть практически реализовано в виде следующего устройства, см. Рис. 2.  Цилиндрический сердечник, сделанный из диэлектрического магнитного материала, с внутренней и с внешней стороны содержит металлические электроды, на которые подаётся переменное электрическое напряжение. Сердечник перемагничивается посредством пропускания переменного тока через навитую на него обмотку (содержащую один или несколько витков). Ниже показана эквивалентная схема запитки устройства, представляющая собой обычный колебательный контур, которая автоматически создаёт условие синфазности колебаний намагниченности сердечника и скорости изменения электрического поля внутри него.  Среднюю силу можно определить по формуле <F> = wM₀E₀V/2с, где M₀ и V – амплитуда намагниченности и объём сердечника. Выражая частоту через длину волны, получим <F> = pM₀E₀V/l . Отсюда найдём среднюю объёмную плотность силы <f>:  

<f> = pM₀E₀/l  (22)

            Как видно из (22), объёмная плотность силы возрастает при уменьшении длины волны, соответствующей частоте напряжения питания.

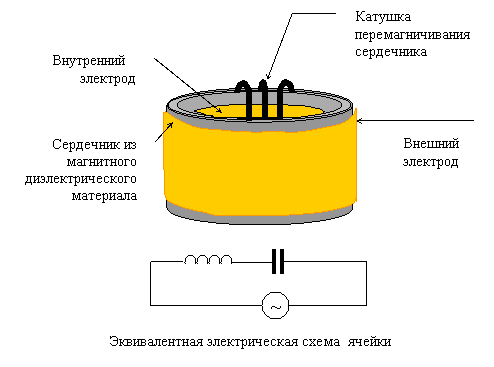
Рис. 2. Устройство, способное совершать неограниченное (инфинитное) ускоренное движение.

            Так как геометрические размеры устройства, работающего в квазистатическом режиме, должны быть, по крайней мере, на порядок меньше длины волны, то для получения больших сил следует использовать структуры, содержащие тысячи и миллионы микроскопических устройств (ячеек), изготавливаемых с применением нанотехнологий (как это делается при изготовлении микросхем).  Элементарные устройства могут выглядеть по-разному, простейшие, например, так, как на Рис. 3 ниже.

Согласно оценочным расчётам при оптимальных технически достижимых параметрах объёмная плотность силы в таких структурах в сантиметровом и миллиметровом диапазонах длин волн может достигать сотен и тысяч килограммов на кубический дециметр (литр) рабочего объёма.

            Описанный способ эфироопорного движения защищён патентом РФ № 2172865 «Способ получения тяги» [8].

3. Законы сохранения импульса и энергии при эфироопорном движении

Закон сохранения импульса (количества движения)

В настоящее время в научной литературе нет единого мнения по вопросам о законах сохранения импульса и энергии в квазистатических электрических и магнитных полях. Попытки дать чёткие конкретные формулировки, как правило, натыкаются на трудности, связанные с нестыковками этих законов сохранения друг с другом и с другими законами физики (см. статью http://www.tts.lt/~nara/paradox/parad.htm ). Например, И. Е. Тамм в [9] утверждает, что «общее количество движения всего статического поля в целом по необходимости равно нулю». Однако проведённые позднее расчёты показали ненулевые результаты, для величины, которую принято называть «импульсом электромагнитного поля»», в том числе и в квазистатике [1], [10].  Методика подобных расчётов на примере магнитно-зарядовых систем продемонстрирована в недавней (2006 г.) работе физика из Принцетона МакДональда, http://puhep1.princeton.edu/~mcdonald/examples/cullwick.pdf .

            Импульсом электромагнитного поля, включая статическое, называют величину

           (23)

Интегрирование производится по всему бесконечному пространству. Если вектор G действительно импульс, то найденные нами равнодействующие F системы двух зарядов (1) и заряда с магнитным диполем (18) должны быть связаны с ним формуле

F = - dG/dt                  (24)

которая, однако, не выполняется, потому что при изменении магнитного поля вектор  G изменяется, а равнодействующая сила  F остаётся прежней. Напомним, что силы, вызванные ускорением зарядов, компенсируют друг друга  (14), а сила индукции, вызванная изменением магнитного момента магнитного диполя (19) компенсируется магнитодинамической силой (20).  Следовательно, равенство (24) не выполняется, вместо него выполняется равенство

F = - (dG/dt)_Н     или    F = - (dG/dt)_w               (25)

Индекс «Н» (или "w") означает, что при взятии производной, магнитное поле (или ускорение зарядов) в (25) следует формально считать постоянной величиной, даже если фактически оно зависит от времени. Следовательно, вектор G не является импульсом электромагнитного поля. Чтобы прояснить его физический смысл раскроем правую часть (25) в соответствии с (23). Получим:

              (26)

Через j = (1/4p)(dE/dt) мы, как это принято, обозначили текущий через вакуум ток смещения Максвелла. Следовательно, подынтегральное выражение есть сила Ампера, действующая на ток смещения, протекающий через единицу объёма физического вакуума, так как будто бы эквивалентный ток протекал по какому-то проводнику. Выходит, что эта сила приложена к самому физическому вакууму, а интеграл в (26) есть реакция равнодействующей системы частиц на физический вакуум. Тогда, закон сохранения импульса можно сформулировать следующим образом:

- «приложенная к системе частиц равнодействующая сила равна по величине и противоположна по направлению силе реакции на физический вакуум, обусловленной суммарной силой Ампера, действующей на токи смещения в магнитном поле, образуемом частицами».

            Таким образом, вектор G фактически является мерой импульса, переданного от вакуума к веществу (системе частиц), вот почему он получил название «потенциальный импульс», [10].

Закон сохранения энергии

Пусть под влиянием равнодействующей F система массой m начинает движение от состояния покоя и приобретает скорость u. Тогда её кинетическая  энергия T = mu²/2.  Но для наблюдателя, по отношению к которому лабораторная система отсчёта движется со скоростью U, кинетическая энергия Т' будет равной:

Т' = m(u + U)²/2 = m(u²/2 + uU + U²/2)

Получилась добавка к энергии 

Т' – Т - mU²/2 = muU    (27)

которая, на первый взгляд, непонятно откуда берётся. Ведь вещественный источник питания не может менять отдаваемую им энергию в зависимости от скорости движения наблюдателя. Следовательно, энергия берётся не от вещественного источника питания, а от физического вакуума и это единственное объяснение, не противоречащее принципу относительности. Вполне естественно, что, коль скоро, наша система движется, отталкиваясь от физического вакуума, значит, она и энергию берет от него же. 

Таким образом, согласно принципу относительности, любое устройство, движущееся под действием силы, имеющей реакцию противодействия на физический вакуум,  совершает работу за счёт убыли энергии физического вакуума.  Это утверждение получило название «теорема об энергии» [10].

            С точки зрения специальной  теории относительности (СТО) Эйнштейна все инерциальные системы отсчёта равноправны  в связи с чем, скорость U в (27) не определена однозначно, что не позволяет сделать заключение о том, сколько именно энергии перешло от физического вакуума к вещественной системе. Иными словами, СТО Эйнштейна не согласована с законом сохранения энергии, которому полностью удовлетворяет теория эфира Лоренца, опубликованная в научной печати на год раньше СТО Эйнштейна. Как уже говорилось во "Введении", теория Лоренца включает в себя тот же самый принцип относительности, на котором построена теория Эйнштейна, совмещённый (в отличие от СТО Эйнштейна) с существованием выделенной системы отсчёта - эфира. Её математический аппарат не отличается от математического аппарата современной классической электродинамики. Кроме этого, теория Лоренца имеет более высокий уровень общности, что позволяет ей решать принципиально новые задачи, не вписывающиеся в рамки СТО Эйнштейна, например задачи эфироопорного движения.

Примечание

*) Сила, действующая на второй диполь со стороны первого F₂₁, равна:

Сила, действующая на первый диполь со стороны второго, получится путём замены R на –R, и перестановки индексов у p₁, p₂. При этом получится F₂₁ = -F₁₂ и F₂₁ + F₁₂ = 0.

СПИСОК ЛИТЕРАТУРЫ

[1] - L. Page and N.I. Adams, Jr., Action and Reaction Between Moving Charges, Am. J. Phys. 13, 141 (1945)

[2] - Л Д. Ландау, Е. М. Лифшиц. Теория поля. Изд-во “Наука”, М., 1973, § 38, § 63, § 9

[3] -  Г. П. Иванов. Пособие для проектирования эфироопорных двигателей. Новая энергетика, № 2 (17), 2004, с. 57-60

[4] - G. Ivanov. A Manual for Designing Ether-based Engines and Devices of Inner-ether Energy. New Energy Technologies, issue 2 (17), June 2004, p. 56-59

[5] -  A. Einstein and J. Laub. Ann. Phys. (Leipzig), 26, 541, (1908)

[6] - С. Р. де Гроот, Л. Г. Сатторп. Электродинамика, М. «Наука», 1982, с. 230-231

[8] - Г. П. Иванов, Ю. Г. Иванов. Способ получения тяги. Патент № 2172865, М., 2001 г

[9] -  И.Е.Тамм. Основы теории электричества. Издательство технико-теоретической     литературы, М.,”НАУКА”, 1989, с. 404-408, 411, 241

[10] - Иванов Г. П. Классическая электродинамика и современность. Висагинас (Литва), 2002 г., можно скачать на http://tts.lt/~nara/aspecty.html

[11] - G.M.Graham, D.G.Lahoz. Nature, 285, 154, 1980.

Георгий Петрович Иванов, 30.12.2007